目录

  1. 多叉堆
  2. 完美的四叉堆？
  3. \(d\log_d n\) 的曲线
  4. \(d\log_d n\) 求导
  5. \(2log_2 n\) 与 \(4log_4 n\)
  6. 性能测试
  7. 结论与困惑
  8. 参考资料

最近在重读左书祺老师的《Go 语言设计与实现》 6.3 计时器一章，书中介绍了 Golang 计时器（Timer）的内部实现 —— 所有的计时器都由每个处理器（runtime.p）单独管理，并通过对应的最小四叉堆进行维护：

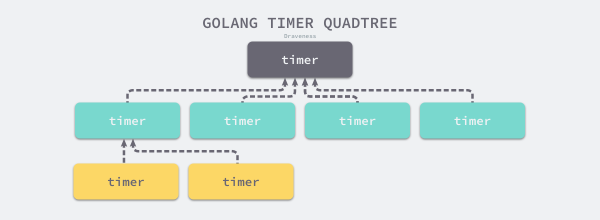
我阅读的开源代码还不够多，因此对于 Golang 使用四叉堆（Quaternary Heap），而非使用经典的二叉堆（Binary Heap）来维护 Timer 感到非常好奇。同时查找一些资料后发现，不光是 Golang 计时器，在不少编程语言的计时器实现中（如 C 语言的 libev 库可以通过编译选项开启四叉堆），以及很多缓存的 LRU 实现中，都用到了四叉堆。

所以，为什么是四叉，而不是二叉、三叉、五叉……？四叉堆究竟有什么神奇之处，本文将做个简单的初探，抛砖引玉，欢迎各位老板进行讨论。

多叉堆

先回顾一下多叉堆，顾名思义，多叉堆是比经典二叉堆叉数更多的堆，每个节点最多会有 d (d>2) 个子节点。d 叉堆（d>2）增加了堆中每个节点的分叉，进而使整个堆的高度变得更低，对于一个节点数量为 n 的 d 叉堆，其高度为 \(\log_d n + O(1)\)。

在 Wiki 和这篇知乎回答中，对于多叉堆与二叉堆相比较的优劣讲得比较清楚了。

d 叉堆（d>2）相对于二叉堆的优势主要有两点：

  • 因为当维护相同数量的元素时，d 叉堆比二叉堆上推节点（sift up）的操作更快。假如最下层某个节点的值被修改为最小，同样上推到堆顶的操作，d 叉堆需要的比较次数只有二叉堆的 \(\log_d 2\) 倍。这也意味着对应堆插入新元素（Insert）时， d 叉堆也比二叉堆更快。
  • 对内存缓存更友好。这也符合直觉，毕竟多叉堆高度更低，其元素内存存储集中在数组前部，表现也更“连续”。而二叉堆对数组的访问范围更大，相对也更“随机”。

而理论上，d 叉堆带来的优势不是没有代价的，这体现在下推（sift down）操作。下推操作涉及到节点与其所有子节点的数值比较。故对于一个 n 元素的 d 叉堆，对应的删除操作（delete）与删除最小值操作（delete-min）其时间复杂度为 \(O(d\log_d n)\) ，很多资料都表示： “代表叉数的 d 值越大，删除操作的时间复杂度越高”。

到这里，我们似乎可以得出结论：“多叉堆与二叉堆互有利弊”，这也符合我们朴素的算法直觉。

但 Wiki 中的一句话引起了我的注意：

“在实践中，四叉堆可能比二叉堆表现得更好，即使是在删除最小元素 delete-min 的操作上。”
“4-heaps may perform better than binary heaps in practice, even for delete-min operations.”

完美的四叉堆？

Wiki 中的这句话意味着，四叉堆在实践中可能是一个可以完美替代二叉堆的方案。我以这句话的引用为线索，经过一段时间的搜寻，但还是没有在互联网找到相关的直接论证与依据。

但我也看到很多人经过性能测试后提出了疑问，比如这个知乎问题， 他基于自己的 C++ 代码测试，在元素个数10000以下时，2叉堆与4叉堆效率差不多；在5w、10w及以上时，4叉堆效率要高于2叉堆。

我自己用 Golang 也写了对比四叉堆与二叉堆的 Benchmark 测试程序，也发现四叉堆不论是插入还是删除，性能都比二叉堆更佳（见后文）。

那么，为什么会这样呢？

Stackoverflow 的这篇回答 似乎给出了令人信服的解释：算法的实际运行，除了要考虑理论的时间复杂度，还要考虑诸多实际硬件环境的影响：

  1. 查找父节点和子节点的成本， 在 d 叉堆中，你可以通过将索引除以 d 来找到你的父节点。对于是 2 的完全幂的 d，这可以通过一个简单、廉价的位移来实现（因为 \(n / 2^k\) = n >> k）。对于奇数或不是 2 的幂的数字，这需要一个除法，这（在某些架构中）比位移更昂贵。（这可能也解释了，为什么很少看到三叉堆在工业中使用，后文也会提到）
  2. 局部性，如今的计算机具有大量的内存缓存层，访问缓存中的内存的成本可能比访问不在缓存中的内存快数百或数千倍。随着在 d 叉堆中增加 d 的值，树的层数变得更少，访问的元素更加靠近，从而提供了更好的局部性。

基于这两点，似乎已经足以解释四叉堆在实践中性能的优异，但当我不经意间画出删除操作时间复杂度对应的 \(d\log_d n\) 的曲线后，发现四叉堆性能优秀的原因可能还有更进一步的解释。

\(d\log_d n\) 的曲线

起初是我在搜索网上关于四叉堆与二叉堆比较的性能 benchmark 报告时找到了萌叔的这篇文章，当时我还很纳闷为什么他针对 Golang Timer 的四叉堆与二叉堆的性能比较只写了 Python 两行代码，然后以为搞错了就没有细看。后来我才发现，文章里的 python 代码计算的是优先队列插入（\(O(log_d n)\)）与删除（\(O(dlog_d n)\)）的时间复杂度。萌叔通过计算不同 d 值对应 d 叉堆的时间复杂度后发现了一个有趣的点：二叉堆与四叉堆对于删除操作的时间消耗似乎是相等的。

在网上关于多叉堆的诸多讨论，很多人都觉得 \(dlog_d n\) 是一个单调递增的函数（当 d > 1, n 不变时），因此 d 叉堆删除的时间复杂度似乎是随着 d 的增大而增大。但当我们画出 \(dlog_d n\) 的曲线（ d > 1 ， n 为固定值 10000,100000,1000000 ）时，发现情况并不是如此：

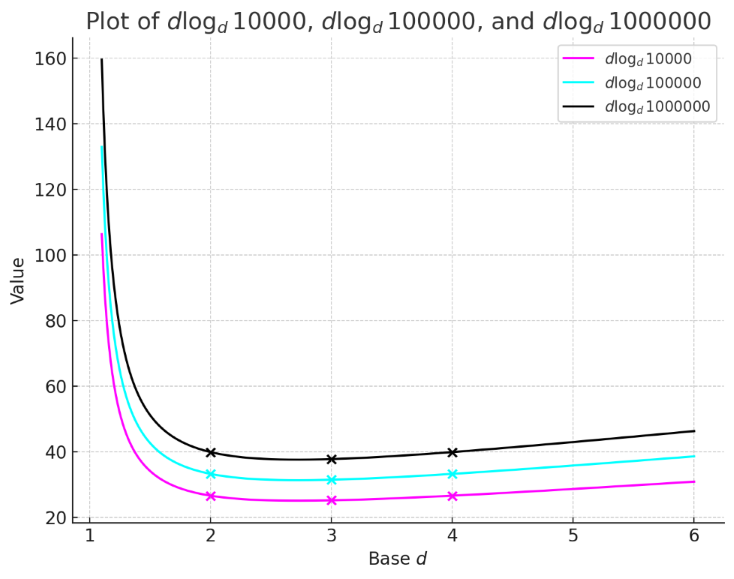
上图是 n=10000,100000,1000000 时，对应的三条 \(d\log_d n\) 曲线，可以发现，在 d=2 与 d=4 之间，函数曲线呈一个向下的小的圆弧。我们放大 d=2 与 d=4 之间的曲线，可以看得更清楚：

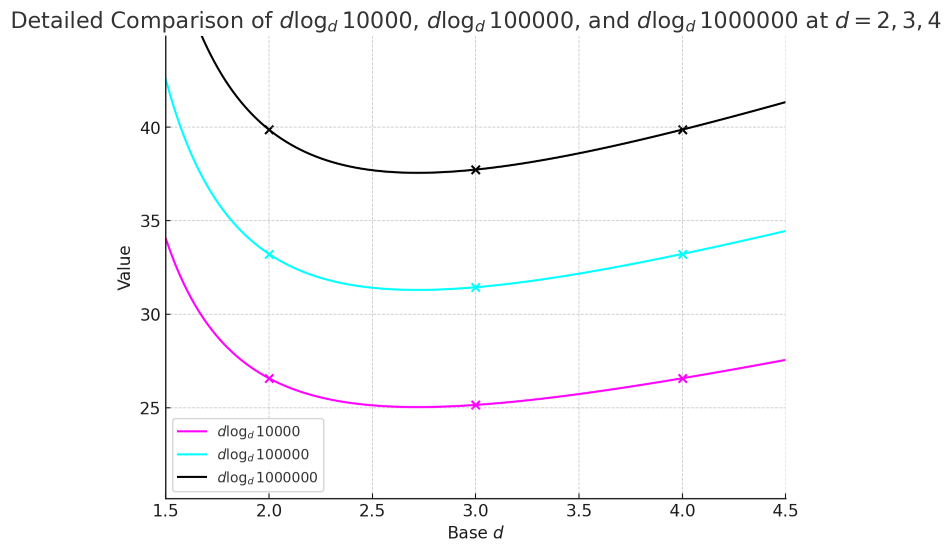
通过观察上述二图我们可以得知，当 \(d \geq 2\) 时，\(d\log_d n\) 并不递增，而是在接近 d=3 的地方存在一个极小值（数学直觉好的老板其实这时候就应该猜到这个 d 是多少了），随后再随着 d 的增加而递增。

下面我们还是用点学校里学过的数学来应证这条曲线 —— 给 \(d\log_d n\) 求个导。

\(d\log_d n\) 求导

根据对数换底公式， \(\log_d n\) 实际可以表示为 \(\frac{\log n}{\log d}\) 。因此我们可以重写 \(d\log_d n\) 为：

$$ d \cdot \log_d n = d \cdot \frac{\log n}{\log d} $$

设 \(f(d) = d \cdot \frac{\log n}{\log d}\)，在这里，我们需要对 d 进行求导，n 我们可以认为是常数。根据导数的乘积法则 ，即 \((fg)’ = f’g + fg’ \)，我们可以推导出 \(f’(d)\)：

$$ f’(d) = d \cdot \left(\frac{\log n}{\log d}\right)’ + (d)’ \cdot \frac{\log n}{\log d} $$

易得：

$$ f’(d) = d \cdot \left(\frac{\log n}{\log d}\right)’ + \frac{\log n}{\log d} $$

下面我们看如何求 \(\left(\frac{\log n}{\log d}\right)’\)，根据求导的链式法则，可得：

$$ \left(\frac{\log n}{\log d}\right)’ = \log n \cdot -\frac{1}{\log^2 d} \cdot \left(\frac{1}{d}\right) = - \frac{\log n}{d \log^2 d}$$

再回过头来看 \(f’(d)\) ：

$$ f’(d) = d \cdot \left(- \frac{\log n}{d \log^2 d}\right) + \frac{\log n}{\log d} = \frac{\log n}{\log d} - \frac{\log n}{\log^2 d} $$

进一步简化可得：

$$ f’(d) = \frac{\log n}{\log d} \cdot \left(1 - \frac{1}{\log d}\right)$$

当 n > 1 时，\(\log n\) 可看作一个大于 0 的常数，因此我们可以通过 \(\frac{1}{\log d} \cdot \left(1 - \frac{1}{\log d} \right)\) 判断 \(f’(d)\)的正负性：

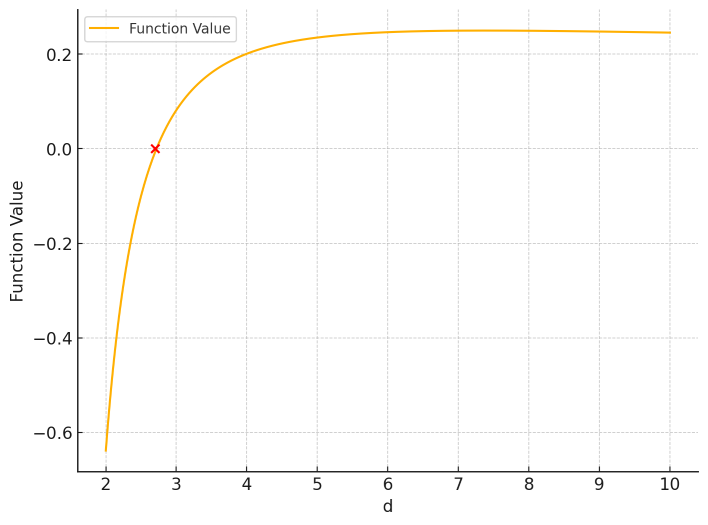
上图是 \(\frac{1}{\log d} \cdot \left(1 - \frac{1}{\log d} \right)\) 的函数曲线图，这里能看到 d 接近 3 时，\(f’(d) \) 函数值为 0。

对于 \(f’(d) = \frac{\log n}{\log d} \cdot \left(1 - \frac{1}{\log d} \right)\) ， 结合上图易得当 \(d = e\) （\(e\) 约为 2.71828 ）时， \(f’(d) = 0\)。

经过上述计算，我们可以简单总结下对应 d 叉堆删除操作的函数 \(f(d) = d\log_d n\) 的特征了：

  • 当 \(0 < d < e\) 时，\(f’(d) < 0\) ，\(d\log_d n\) 的函数值将随着 d 的增加而减少
  • 当 \( d = e \) 时，\(f’(d) = 0\)， 函数 \(d\log_d n\) 为极小值，其值为 \(e \cdot \log n \)
  • 当 \(d > e \) 时 , \(f’(d) > 0\)， \(d\log_d n\) 的函数值将随着 d 的增加而增加

现在我们已经可以确认，当 \(d \geq 2\) 时， \(d\log_d n\) 的值并不是一味随着 d 的增加而增加的。进一步地，我们直接来看下二叉堆与四叉堆，比较一下它们二者删除操作对应的算法复杂度函数，即 \(2log_2 n\) 与 \(4log_4 n\)。

\(2log_2 n\) 与 \(4log_4 n\)

萌叔的文章 通过代码测试指出 \(2log_2 n\) 与 \(4log_4 n\) 是相等的，下面我们简单来推导下。

我们直接看下 \(4log_4 n\) ， 根据对数换底公式，我们可得：

$$ 4log_4 n = 4 \cdot \frac{log_2 n}{log_2 4} = 2log_2 n $$

可见，对于二叉堆与四叉堆，它们在 delete-min 操作的时间复杂度在理论上是相等的。而四叉堆又具有更好的局部性，在实际运行中，其删除性能很可能比二叉堆更优。再加上四叉堆本身在插入操作（\(O(log_d n)\)）相对二叉堆的性能优势，可以看出四叉堆在工业上确实是一个可以完美代替二叉堆的方案。

既然二叉堆与四叉堆删除的复杂度相等，再结合前文我们对于 \(d\log_d n\) 的求导计算，理论上删除性能最优的应该是三叉堆。但在工业上很少看到三叉堆的方案，我没有做过性能测试，但我想一个主要原因应该就是前文提到的查找父节点和子节点的成本。4 是 2 的完全幂，四叉堆可以用移位操作来寻找父节点与子节点， 但 3 不是 2 的完全幂，三叉堆查找父节点与子节点需要用到乘除，多出了额外的硬件指令开销，而这些开销很可能是实际程序运行时不容忽视的。

以此类推，下一个属于 2 的完全幂的就是八叉堆了，但其 delete-min 操作理论上相对于二叉堆与四叉堆已经开始带来一定的性能损失。

综合上述各项因素考虑，四叉堆在多叉堆中确实是最理想合适的方案。工业上如此中意四叉堆，也有了对应的合理解释。

性能测试

下面我们通过一个简单的 benchmark 来直接比较四叉堆与二叉堆的性能，以印证前文的部分结论。

首先是 heap.go ，该文件实现了最小二叉堆（MinBinaryMap）与最小四叉堆（MinQuaternaryHeap），以及对应的插入（Insert）和提取最小值（ExtractMin）操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
// heap.go
package heap_benchmark


type MinBinaryHeap struct {
    data []int
}

// 插入新元素
func (h *MinBinaryHeap) Insert(value int) {
    h.data = append(h.data, value)  // 将新元素添加到数组末尾
    h.siftUp(len(h.data) - 1)      // 将新元素向上调整到合适位置
}

// 提取最小元素
func (h *MinBinaryHeap) ExtractMin() (int, bool) {
    if len(h.data) == 0 {
        return 0, false
    }
    min := h.data[0]
    lastIndex := len(h.data) - 1
    h.data[0] = h.data[lastIndex]  // 将最后一个元素移动到根位置
    h.data = h.data[:lastIndex]    // 移除数组中最后一个元素
    h.siftDown(0)                  // 将新的根元素向下调整到合适位置
    return min, true
}

// 向上调整元素
func (h *MinBinaryHeap) siftUp(index int) {
    for index > 0 {
        parent := (index - 1) / 2  // 二叉堆的父节点索引
        if h.data[index] < h.data[parent] {
            h.data[index], h.data[parent] = h.data[parent], h.data[index]
            index = parent
        } else {
            break
        }
    }
}

// 向下调整元素
func (h *MinBinaryHeap) siftDown(index int) {
    last := len(h.data) - 1
    for {
        left := 2*index + 1    // 左子节点索引
        right := left + 1      // 右子节点索引
        smallest := index

        if left <= last && h.data[left] < h.data[smallest] {
            smallest = left
        }
        if right <= last && h.data[right] < h.data[smallest] {
            smallest = right
        }

        if smallest != index {
            h.data[index], h.data[smallest] = h.data[smallest], h.data[index]
            index = smallest
        } else {
            break
        }
    }
}

type MinQuaternaryHeap struct {
    data []int
}

// 插入新元素
func (h *MinQuaternaryHeap) Insert(value int) {
    h.data = append(h.data, value)  // 将新元素添加到数组末尾
    h.siftUp(len(h.data) - 1)      // 将新元素向上调整到合适位置
}

// 提取最小元素
func (h *MinQuaternaryHeap) ExtractMin() (int, bool) {
    if len(h.data) == 0 {
        return 0, false
    }
    min := h.data[0]
    lastIndex := len(h.data) - 1
    h.data[0] = h.data[lastIndex]  // 将最后一个元素移动到根位置
    h.data = h.data[:lastIndex]    // 移除数组中最后一个元素
    h.siftDown(0)                  // 将新的根元素向下调整到合适位置
    return min, true
}

// 向上调整元素
func (h *MinQuaternaryHeap) siftUp(index int) {
    for index > 0 {
        parent := (index - 1) / 4  // 四叉堆的父节点索引
        if h.data[index] < h.data[parent] {
            h.data[index], h.data[parent] = h.data[parent], h.data[index]
            index = parent
        } else {
            break
        }
    }
}

// 向下调整元素
func (h *MinQuaternaryHeap) siftDown(index int) {
    last := len(h.data) - 1
    for {
        child := 4*index + 1  // 第一个子节点
        if child > last {
            break
        }

        // 找到四个子节点中的最小节点
        minChild := child
        for i := 1; i <= 3; i++ {
            if child+i <= last && h.data[child+i] < h.data[minChild] {
                minChild = child + i
            }
        }

        if h.data[minChild] < h.data[index] {
            h.data[index], h.data[minChild] = h.data[minChild], h.data[index]
            index = minChild
        } else {
            break
        }
    }
}

然后是 heap_test.go ，实际运行 benchmark 的测试文件，包含了性能测试四叉堆与二叉堆操作的用例。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
// heap_test.go
package heap_benchmark

import (
    "testing"
    "math/rand"
)

const N = 10000000

// 为二叉堆插入元素的基准测试
func BenchmarkBinaryHeapInsert(b *testing.B) {
    var heap MinBinaryHeap
    rand.Seed(42) // 确保每次基准测试的随机数都是相同的

    b.ResetTimer()
    for i := 0; i < b.N; i++ {
        heap.Insert(rand.Intn(100000))
    }
}

// 为二叉堆移除元素的基准测试
func BenchmarkBinaryHeapExtractMin(b *testing.B) {
    var heap MinBinaryHeap
    // 预先填充堆
    for i := 0; i < N; i++ {
        heap.Insert(rand.Intn(100000))
    }
    
    b.ResetTimer()
    for i := 0; i < b.N; i++ {
        heap.ExtractMin()
    }
}

// 为四叉堆插入元素的基准测试
func BenchmarkQuaternaryHeapInsert(b *testing.B) {
    var heap MinQuaternaryHeap
    rand.Seed(42) // 确保每次基准测试的随机数都是相同的

    b.ResetTimer()
    for i := 0; i < b.N; i++ {
        heap.Insert(rand.Intn(100000))
    }
}

// 为四叉堆移除元素的基准测试
func BenchmarkQuaternaryHeapExtractMin(b *testing.B) {
    var heap MinQuaternaryHeap
    // 预先填充堆
    for i := 0; i < N; i++ {
        heap.Insert(rand.Intn(100000))
    }

    b.ResetTimer()
    for i := 0; i < b.N; i++ {
        heap.ExtractMin()
    }
}

测试基于 Go 1.22 ，运行环境为 Windows 11, Intel(R) Core(TM) i9-14900KF

通过命令行我们进入上述两个 go 文件所在目录，运行 benchmark 命令：

1
go test -bench="."

结果如下：

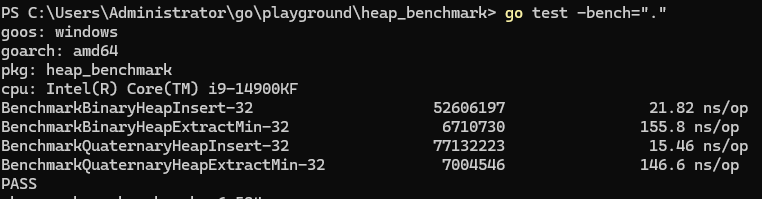
可见四叉堆的插入与提取最小值操作性能都优于二叉堆，与我们前文所得到的结论一致。

结论与困惑

至此，我们可以得到以下几个结论：

  1. 理论上，四叉堆的插入性能比二叉堆更优，而提取最小值操作的时间复杂度二者相等。加上四叉堆运行在实际硬件中局部性更优，因此就性能角度而言，四叉堆在实践中是一个可以完美替代二叉堆的方案。
  2. 理论上，三叉堆的提取最小值性能为多叉堆中最优。但实际运行中，三叉堆查找父节点和子节点时无法通过移位操作优化性能，这可能是它在工业上很少被使用的原因。与之相对，四叉堆的查找父子节点操作可以被移位操作优化。
  3. 理论上，四叉堆之后，多叉堆的提取最小值操作的性能都逐步有所下降，且考虑移位操作优化的问题，可选的方案就更少了。
  4. 结合理论与实践综合来看，四叉堆是多叉堆中，在多数通用场景下性能最优的方案，也因此被各类项目频繁选用。

行文至此，我的困惑在于上述结论不难得出（数学求导并不复杂），但我却没有找到相对严谨通过计算推导时间复杂度来评估多叉堆性能的文章，也没找到工业中选用四叉堆的有力理论支撑。相反，不管是中文互联网还是海外，对于选用四叉堆的原因解释都是比较含糊，甚至不少是与本文提到的结论相悖的。

不知是我推导出了问题得到了错误的结论，还是我其实没找到真正支撑工业界使用四叉堆的文献资料。

如果有哪位老师觉得我的推导有问题，或是知道哪里有更好更权威讨论多叉堆的材料以补充上述结论的，欢迎联系我或者在 GitTalk 留言。

参考资料