【Go 语言编程珠玑】deBruijn 序列快速计算 64 位二进制数末尾多少个 0

目录

1. de Bruijn 序列
2. TrailingZeros64 源码分析
3. 总结
4. 参考资料

起因是在读 Golang Malloc 相关代码时候，看到了 sys.TrailingZeros64 标准库函数，这个函数的作用是计算传入的 64 位二进制数（uint64）末尾有多少个 0。

计算二进制末尾有多少个 0，似乎很简单没啥好多讲的，直觉第一反应是类似这么实现：

func countTrailingZeros(n uint64) int {
  if n == 0 { return 64 }
  count := 0
  for n > 0 {
    if n & 1 == 0 {
      count++
    } else {
      break
    }
    n >>= 1
  }
  return count
}

就是不断循环看数的最低位，如果是 0 则计数并将数右移，如果是 1 则退出循环，返回计数。道理和循环不断模 2 取余计数然后除以 2 是一样的。

但 Golang 标准库 sys.TrailingZeros64 的实现完全不是这样：

// runtime/internal/sys/intrinsics.go
var deBruijn64tab = [64]byte{
	0, 1, 56, 2, 57, 49, 28, 3, 61, 58, 42, 50, 38, 29, 17, 4,
	62, 47, 59, 36, 45, 43, 51, 22, 53, 39, 33, 30, 24, 18, 12, 5,
	63, 55, 48, 27, 60, 41, 37, 16, 46, 35, 44, 21, 52, 32, 23, 11,
	54, 26, 40, 15, 34, 20, 31, 10, 25, 14, 19, 9, 13, 8, 7, 6,
}

const deBruijn64 = 0x03f79d71b4ca8b09

// TrailingZeros64 returns the number of trailing zero bits in x; the result is 64 for x == 0.
func TrailingZeros64(x uint64) int {
	if x == 0 {
		return 64
	}
	return int(deBruijn64tab[(x&-x)*deBruijn64>>(64-6)])
}

这个函数似乎是将 x 进行了一套位运算，然后乘了一个 magic number（0x03f79d71b4ca8b09），进行位移后再基于一张表（deBrujin64tab）进行映射就得到了 x 末尾 0 的数量。

这个实现乍看非常神奇，也确实会比我们朴素的循环写法要快不少。然后我想起来之前在阅读张富春老板的博客 时也看到了关于这个函数的讨论。

函数源码的注释介绍了实现的思路，但我比较菜，看完还是有些云里雾里，不知道如何做到的 (lll￢ω￢)：

// If popcount is fast, replace code below with return popcount(^x & (x - 1)).
//
// x & -x leaves only the right-most bit set in the word. Let k be the
// index of that bit. Since only a single bit is set, the value is two
// to the power of k. Multiplying by a power of two is equivalent to
// left shifting, in this case by k bits. The de Bruijn (64 bit) constant
// is such that all six bit, consecutive substrings are distinct.
// Therefore, if we have a left shifted version of this constant we can
// find by how many bits it was shifted by looking at which six bit
// substring ended up at the top of the word.
// (Knuth, volume 4, section 7.3.1)

 // 如果 popcount 运算速度快，可以用 return popcount(^x & (x - 1)) 替换下面的代码。
 //
 // x & -x 仅保留数中最右侧的值为 1 的位。设该位的下标为 k。
 // 由于只有一个位被设置，因此 x & -x 计算得到值等于 2 的 k 次方。乘以 2 的幂等同于
 // 左移，这里就是左移 k 位。de Bruijn 常量（64 位）具有这样的特性：
 // 所有的六位连续子串都是唯一的。因此，如果我们有一个左移版本的此常量，
 // 我们可以通过查看哪个六位子串位于左移常量的顶部来确定它被左移了多少位。
 // （出自 Knuth 的《计算机程序设计艺术》第 4 卷，第 7.3.1 节）

这个算法原来还来自 Knuth 大师大名鼎鼎的 The Art of Computer Programming ，而在中文互联网却很少有这个算法的直接资料，实在让我有些好奇。加上这两天在 V2EX 看到个帖子《你见过哪些好玩又花里胡哨的代码呢》 ，所以就决定好好探究学习一下，弄明白之后顺便水个帖子（x

函数代码 magic number 的变量名称以及注释中都提到了 de Bruijn 常量，那么就先从理解这个数开始吧。

de Bruijn 序列

代码里的 de Bruijn 数，相当于一个 de Bruijn 序列，我们看 Wikipedia 关于 de Bruijn 序列的介绍：

In combinatorial mathematics, a de Bruijn sequence of order \(n\) on a size-\(k\) alphabet \(A\) is a cyclic sequence in which every possible length-n string on \(A\) occurs exactly once as a substring (i.e., as a contiguous subsequence).
Such a sequence is denoted by \(B(k, n)\) and has length \(k^n\), which is also the number of distinct strings of length \(n\) on \(A\).
在组合数学中，一个在大小为 \(k\) 的字母表 \(A\) 上的 \(n\) 阶 de Bruijn 序列是一个循环序列，其中每个可能的长度为 \(n\) 的 \(A\) 上的字符串恰好作为子串（即，作为一个连续的子序列）在这个 de Bruijn 序列中出现一次。
这样的序列记作 \(B(k, n)\)，其长度为 \(k^n\)，这也是字母表 \(A\) 里长度为 \(n\) 的字符串的总数。

要注意的是，de Bruijn 序列并不一定要由数字组成，可以是由字符组成的。它的核心特性就是，包含了特定字符集（字符集大小为 k）长度为 n 的所有可能的序列，且每个作为子序列在 deBruijn 序列中有且仅出现一次。

我们看一个 Wiki 提供的最简单的例子：

上图有字母表 \(A \{0,1\}\)，有0,1两个元素即 \(k=2\)。然后我们有 deBruijn 循环序列 0011，包含字母表 A 对应长度为 2 （\(n=2\)）所有可能的序列：00, 01, 11, 10。

同时，该 deBruijn 循环序列总长度为 \(2^2=4\)，其子序列与长度为 2 的所有可能序列是一一对应的，也就是说，从该 deBruijn 循环序列的任意位开始顺序取两个元素，恰好对应一个长度为 2 的子序列，且每个对应子序列不同。

deBruijn 相当于浓缩了所有长度为 n 的子序列，而它的构建却不算很复杂，那就是先构建一个对应 \(B(k, n-1)\) 的 deBruijn 图，然后计算其欧拉回路。

还是 Wiki 中介绍的例子，若我们要构建一个 \(A \{0,1\}, B(2,4)\) 的 deBruijn 序列，那么可以先构建一个 \(B(2,3)\) 的 deBruijn 图：

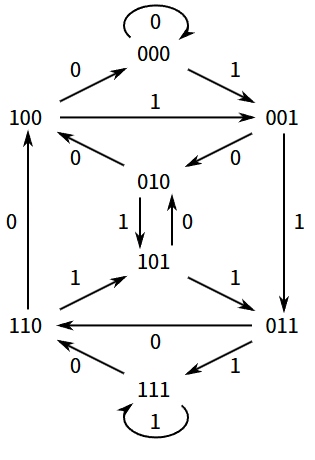
可以看到，deBruijn 是个有向图， \(B(2,3)\) 的 deBruijn 图有 \(2^3=8\) 个节点，每个节点的值即代表一个长度为 \(n=3\) 的序列，每个节点的入度与出度都为 2。连接节点的有向边代表节点对应序列的转换，相当于节点值左移 1 位（无回绕），然后加上对应边的权重， 如 \(001 \rightarrow 011\) 这条边的权重为 1，代表 (001 << 1) + 1 = 011。

接下来，我们求这个 deBruijn 图的欧拉回路（每条边恰好经过一次且最终回到起点的路径），就能得到一个 \(B(2,4)\) 的 deBruijn 序列：

可以看到如上图所示，我们记录起始节点的值，然后按顺序追加记录欧拉回路遍历边的权重，就能得到 \(B(2,4)\) deBruijn 序列 0000111101100101

当我们聚焦 \(k=2\) 的场景，可以发现在一个 \(B(2,n)\) deBruijn 循环序列中，囊括了所有 n 位二进制数。这是个非常重要的特性，也是计算 64 位整数末尾 0 算法的基础。

TrailingZeros64 源码分析

我们再回到 sys.TrailingZeros64 函数，这下我们明白全局变量 deBruijn64 其实就是一个 \(B(2,6)\) deBruijn 序列，其二进制值表示 0000001111110111100111010111000110110100110010101000101100001001，我们可以写一个简单的程序，将它的所有六位二进制子序列全部输出来：

package main

import "fmt"

func main() {
	var num uint64 = 0x03f79d71b4ca8b09
	var subn uint64
	for i := 0; i < 64; i++ {
		subn = num >> 58
		fmt.Printf("%06b", subn)
		if i%8 == 7 {
			fmt.Printf("\n")
		} else {
			fmt.Printf("\t")
		}
		num <<= 1
	}
}

可以得到 64 个六位二进制数，如果仔细比对的话，这 64 个数都是不同的，即所有的六位二进制数：

000000	000001	000011	000111	001111	011111	111111	111110
111101	111011	110111	101111	011110	111100	111001	110011
100111	001110	011101	111010	110101	101011	010111	101110
011100	111000	110001	100011	000110	001101	011011	110110
101101	011010	110100	101001	010011	100110	001100	011001
110010	100101	001010	010101	101010	010100	101000	010001
100010	000101	001011	010110	101100	011000	110000	100001
000010	000100	001001	010010	100100	001000	010000	100000

这里有个注意点那就是左移操作事实上不会发生位的循环回绕（wrap around），但由于第一个子序列数为 000000，即便左移操作没发生回绕，由于第一个子序列都是 0，也可以视作发生了循环回绕，所以不影响。

现在我们再来看整体的计算 deBruijn64tab[(x&-x)*deBruijn64>>(64-6)] 。

首先就是 x&-x， -x 相当于 x 的负数值，即 x 的补码，也就是 x 值按位取反然后再加 1。因此 x&-x 相当于只保留 x 最右侧的 1，把其他位都清零了（不确定的小伙伴可以自己拿草稿纸算算验证下）。

由于 x&-x 只保留 x 原先最右侧的 1，所以相当于 x&-x 算出来的值必然是 2 的幂，我们设 x&-x = 1 << k， 那么 (x&-x)*deBruijn64 相当于 deBruijn64 << k， 而仔细想一下， x&-x 相当于只保留 x 最右侧的 1，那么这里的 k 也就代表了 x&-x 末尾有多少个 0，即 x 末尾有多少个 0。

(x&-x)*deBruijn64 相当于 deBruijn64 << k。k 代表末尾有多少个 0，k 的取值范围为 [0, 64] ，显而易见，不同的 k，其 (deBruijn64 << k) >> (64-6) 的值能得到不同且唯一对应的六位二进制值，那么先将这个六位二进制值对应 k 值记录在一个 map 里（deBruijn64tab），算出子序列的值之后一查，就能得到 k 值，即 x 的末尾有多少个 0 了。

综上，TrailingZeros64 计算末尾 0 数量的流程就完成了。

总结

当明白 TrailingZeros64 基于 deBrujin 序列的计算原理之后，在感到豁然开朗之余，不免感到人类的智慧时常会超出我自己的想象。虽然自己愚钝远远称不上聪明，但只要持续学习与探究，还是能感受到一点点数学之美的。

参考资料

• Wikipedia - deBruijn sequence: https://en.wikipedia.org/wiki/De_Bruijn_sequence
• 神秘常量0x077CB531，德布莱英序列的恩赐: https://www.cnblogs.com/xiaohutu/p/10950011.html
• 如何计算一个uint64类型的二进制值的尾部有多少个0 : https://www.cnblogs.com/ahfuzhang/p/15900551.html
• de Bruijn CTZ with proper handling of 0 : https://gist.github.com/resilar/e722d4600dbec9752771ab4c9d47044f